Gli enigmi matematici sono tra i più complessi e affascinanti mai creati. Alcuni hanno resistito per secoli prima che una soluzione venisse trovata, mentre altri sono ancora aperti, in attesa di una mente brillante che possa risolverli.
Il problema dei sette ponti di Königsberg
Uno dei più noti enigmi matematici è quello dei sette ponti di Königsberg. La città di Königsberg (oggi Kaliningrad) era attraversata da un fiume con sette ponti. L'enigma chiedeva se fosse possibile attraversare tutti i ponti una sola volta senza mai tornare sui propri passi. Il matematico Leonhard Euler dimostrò che era impossibile, gettando le basi per la teoria dei grafi, oggi essenziale in molte applicazioni tecnologiche.
L'ultimo teorema di Fermat
Un altro enigma famoso è l'ultimo teorema di Fermat, proposto dal matematico Pierre de Fermat nel XVII secolo. Fermat affermò di avere una "meravigliosa dimostrazione" per il teorema, ma non la scrisse mai. Ci vollero oltre 350 anni prima che Andrew Wiles riuscisse a dimostrarlo nel 1994.
Gli enigmi della crittografia
Molti enigmi matematici sono collegati alla crittografia, la scienza della cifratura. Dai codici della Seconda guerra mondiale alle moderne chiavi di sicurezza online, la risoluzione di enigmi matematici è diventata essenziale per garantire la sicurezza dei dati digitali.
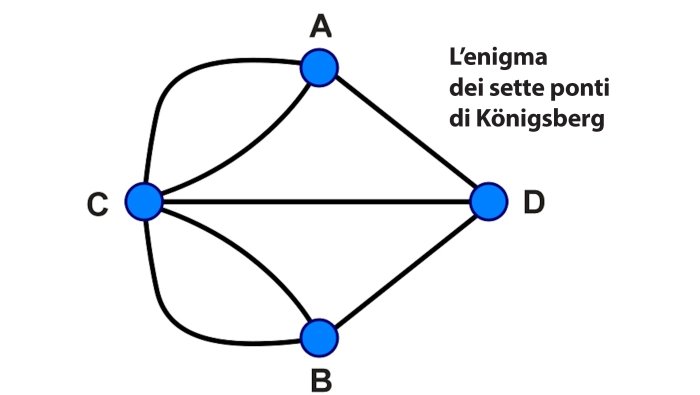
Ecco la soluzione di Euler al problema dei sette ponti
Euler dimostrò che non esiste una soluzione al problema. Egli lo fece riducendo la mappa della città a un grafo, in cui le isole e le sponde erano rappresentate come nodi e i ponti come archi che collegavano i nodi. Euler scoprì che, affinché un tale percorso (detto ciclo euleriano) esista, ogni nodo del grafo deve avere un numero pari di archi che lo attraversano (deve essere di grado pari), tranne al massimo due nodi, che potrebbero essere di grado dispari (per permettere di partire da un nodo e finire in un altro diverso).
Nel caso dei ponti di Königsberg, tutti i nodi (le sponde e le isole) avevano un numero dispari di archi. In particolare, i quattro nodi avevano i seguenti gradi:
Sponda nord: 3 archi (dispari)
Sponda sud: 3 archi (dispari)
Isola grande: 5 archi (dispari)
Isola piccola: 3 archi (dispari)
Poiché tutti i nodi avevano un numero dispari di archi, non era possibile trovare un percorso che attraversasse ogni ponte una sola volta.
Conclusione: non esiste una soluzione per il problema dei sette ponti di Königsberg. Euler introdusse, con questa dimostrazione, la teoria dei grafi, dando origine a uno dei rami più importanti della matematica moderna.